티스토리 뷰
오늘은 이진 탐색에 대해 알아보자.
이 포스팅의 학습 목표
- 이진 탐색 사용의 이유를 이해한다.
- 이진 탐색의 구조를 이해하고, 적용할 수 있다.
탐색 알고리즘을 왜 배워야 할까?
저장된 데이터를 활용하기 위해선, 원하는 데이터를 정확하게 가져와야 한다. 데이터가 한두 개라면, 한눈으로도 확인이 가능하다. 10개 정도라면, 순차적으로 확인하며 보는 것도 어렵지 않다. 하지만, 데이터가 2만 개, 3만 개라면? 찾는 것만으로도 엄청난 시간이 요소 될 것이다. 만약, 10만 개의 데이터 중 하나를 데이터를 활용하려면, 활용은 커녕 찾는데만 시간을 모두 쏟게 될 수도 있다. 그래서 이러한 시간 소요를 줄여보고자 해결책을 내놓은 것들이 탐색 알고리즘이다.
아래의 접은 글은 간단한 선형 탐색에 대한 프리뷰이다. 이해가 필요하다면 참고하자.
선형 탐색 VS 이진 탐색
이진 탐색에 앞서, 일반적으로 비교되는 선형 탐색에 대해 간단히만 얘기하고 넘어가겠다. 선형 탐색은 모든 데이터를 하나씩 순차적으로 탐색하는 것이다. 운 좋게 중간에 찾을 수도 있지만, 최악의 경우엔 모든 데이터에 접근을 해야 한다.

위의 그림과 같이 순차적으로 접근하기에 데이터 수의 비례한 시간이 소요된다. 10만 개의 데이터라면, 10만 개를 모두 확인해하는 상황이 나올 수도 있다. 이진 탐색은 이런 미친듯한 접근 횟수를 줄여준다.
이진 탐색
자, 그럼 이진 탐색이 무엇인지 알아보자. 이진 탐색의 핵심은 '반으로 쪼개서 생각하기'이다. 반으로 잘라서 중앙값에 있는 데이터가 내가 원하는 데이터보다 앞에 있는지 뒤에 있는지 확인한다. 데이터 위치에 따라 반으로 쪼갠 데이터 중 한쪽만 확인해가며, 내가 원하는 데이터로 접근하는 방식이다.
여기서 의문이 들 수 있다.
"인덱스로 접근해서, 내 앞에 있는 녀석의 값이 큰지, 작은 지는 확인을 할 수가 없잖아?"
"그러면 반으로 쪼개도 의미가 없는 거 아냐?"
정확하다. 백날 반으로 쪼개서 찾아보려고 해 봐야, 뒤죽박죽으로 박혀있으면, 중앙값이 무의미해진다.
그래서 이진 탐색은 반드시 정렬이 전제조건이다. 정렬되어 있는 데이터에 대해서만, 중앙값을 중심으로 비교가 가능해지기 때문이다.
예제를 통해, 좀 더 확실하게 이해하자
1부터 15중에 나는 숫자 4를 찾고 싶다고 가정해보자. 그림으로 표현하면 다음과 같을 것이다.

이 데이터를 이진 탐색하기 위해서, 전체를 반으로 가를 것이다. 이것은 처음과 끝 데이터의 중앙값을 선택한다는 소리다. 표현하면 아래와 같다.
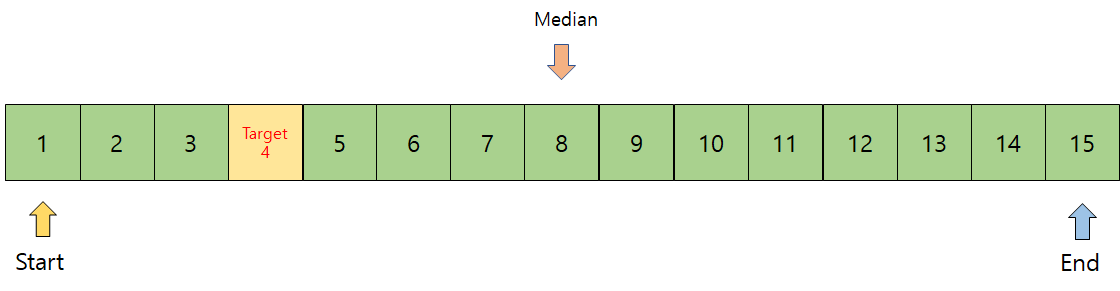
이제 기준점으로 8이라는 데이터가 나왔다. 그럼 8이라는 데이터가 내가 원하는 데이터 4와 크기 비교를 통해
데이터 4가 중앙값에서 왼쪽에 있는지, 오른쪽에 있는지 판단한다.
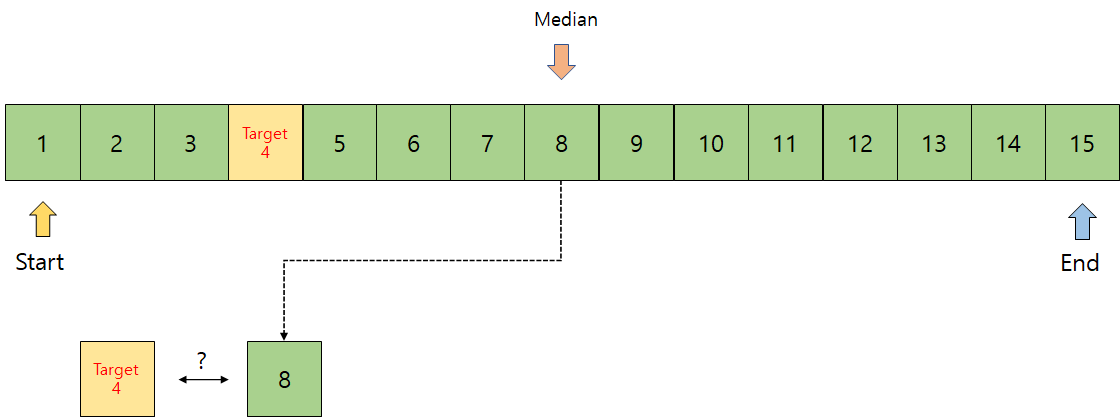
그림과 같이 데이터 4는 중앙값을 중심으로 왼편에 있다. 오른쪽은 쓸모가 없으니, 왼쪽 범위만 사용하기 위해 End의 위치를 옮겨서, 지금까지의 행동을 데이터 4를 찾을 때까지 반복하면 된다. 한번 더 이진 탐색을 하면 아래와 같다.
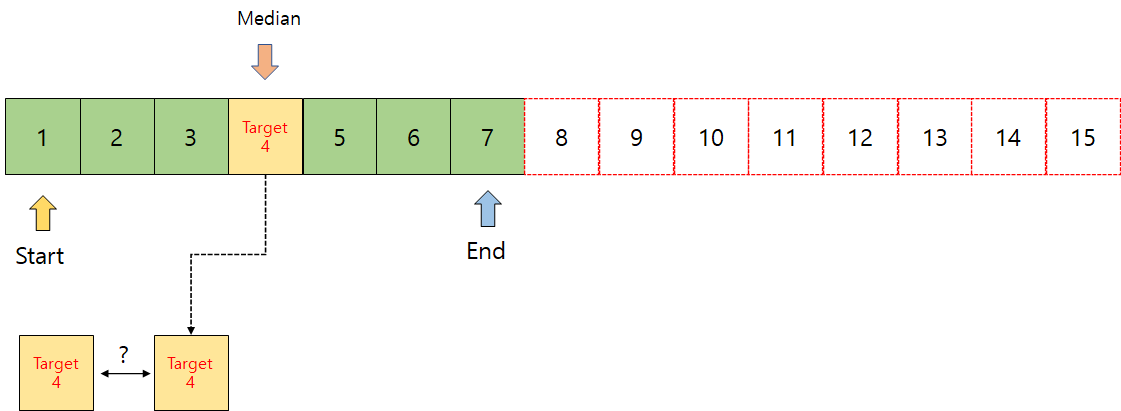
그럼 이제 데이터 1과 데이터 7을 기준으로 중앙값을 잡는다. 확인해보니, 데이터 4와 중앙값이 일치한다. 찾았다.
이런 식으로 반으로 쪼개서 계속 생각하게 된다.
빠르다는 느낌은 느꼈을 수도 있고, 못 느꼈을 수도 있다. 이 느낌을 정확하게 가져가기 위해 수치화해보겠다.
16개 중에서 1개의 데이터를 이진 탐색으로 찾을 때, 최악의 경우를 생각해보자.
처음 반으로 쪼개서 못 찾았다. 다시 8개 중 찾아야한다.(16 / 2)
처음 반으로 쪼개서 못 찾았다. 다시 4개 중 찾아야한다.(8 / 2)
처음 반으로 쪼개서 못 찾았다. 다시 2개 중 찾아야한다.(4 / 2)
처음 반으로 쪼개서 못찾았다. 다시 1개 중 찾아야 한다.(2 / 2)
횟수가 증가할수록 절반(1/2)으로 들어오는 게 눈으로 보일 것이다. 이것을 더 정확하게 식으로 표현해보자.
이 경우를 일반화해서 생각해보자. N개의 데이터가 있을 때, 최악의 경우 탐색을 진행하는 횟수를 k 라 해보자.
그럼 아래와 같은 식으로 나타낼 수 있다.
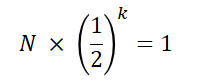
그럼 이 식을 N에 대한 식으로 바꿔보자.
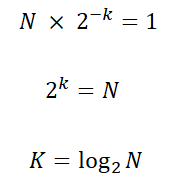
데이터가 N개 일 때, log 2N의 시행 횟수를 가진다. N이 1024만 돼도 선형 탐색으로 1024번 확인해야 하지만, 이진 탐색으로는 단, 10번이면 끝내는 문제가 된다. 데이터가 클수록, 선형 탐색보다 미라클 한 속도를 보여준다. 이해를 더 돕기 위해 그래프로 표현해봤다.
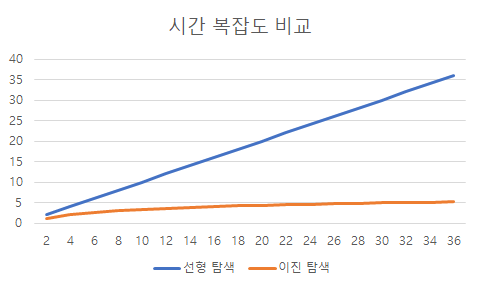
데이터가 많을수록, 차이가 더 극명해지는 것을 볼 수 있다.
그럼 이제까지 구조에 대해 알아보았으니, 사용법에 대해서 생각해보자. 이제까지 배운 것들을 거꾸로 생각하면 필요한 것이 보인다.
- 원하는 값을 찾기 위해선 중앙값을 알아야 한다.(그래야 비교하니까)
- 중앙값을 알려면, 양쪽의 기준(범위)을 알아야 한다(그림에서 Start, End)
- 원하는 값이 어디 있는지에 따라, 기준의 범위를 바꿔야 한다.
굉장히 어려울 것 같지만 핵심은 이것이 전부다. 이 정도만 이해하고 있다면, 충분히 사용 가능할 것이다.
코드를 짜는 연습을 하고 싶다면, 접은 글을 보면 도움이 될 것 같다.
위의 요구사항을 만족하는 메서드를 만들어보면 아래와 같다.
//이진 탐색
public static int binarySearch(int start,int end,int target){
int mid = (start+end)/2;
//중앙값이 원하는 값이면 바로 반환
if(mid == target){
return mid;
}
//값이 없을 때 반환
if(start > end){
return -1;
}
//타겟이 중앙값 보다 왼쪽
if( mid > target){
//기준 범위가 왼쪽이 될 수 있게 end 변경
end = mid -1;
}else{
//타겟이 중앙값 보다 오른쪽
//기준 범위가 오른쪽이 될 수 있게 start 변경
start = mid+1;
}
int result = binarySearch(start,end,target);
return result;
}
위 메서드는 일치하는 데이터를 찾을 때까지, 재귀적으로 호출한다.(전형적인 재귀 함수다.) 중앙값을 기준으로 기준 범위 start와 end를 조절하면서, 반으로 쪼개 나간다. 결과를 찾거나, 혹은 데이터가 없어 start와 end가 역전되었을 경우에 반환 값을 돌려주게 된다. 이런 식으로 요구사항을 생각하면서 함수를 만들면 비교적 쉽게 만들 수 있다.
그럼 저 함수를 활용한 예제를 하나 풀어보면 좋을 것 같다.
1000개의 정수형 배열 중에서 원하는 데이터 하나를 정하고 이진 탐색을 시행한다. 그때 수행하는 이진 탐색 횟수를 알아보자. (배열은 자기 자신의 인덱스를 값으로 가지고 있다.)
코드
public class Binary {
public static void main(String[] args) {
int size = 1000;
int target = (int)(Math.random()*size);
int[] data = new int[size];
for (int i = 0 ; i < data.length ;i++){
data[i] = i;
}
System.out.println(" "+size+"개 짜리 데이터를 가진 배열이 생성되었습니다.");
System.out.println("타겟 데이터 : "+target+" \t 찾아주세요.");
int start = 0;
int end = data[size-1];
int answer = binarySearch(start,end,target,0);
System.out.println("데이터를 찾았습니다 : " + answer + "회 탐색 시행");
System.out.println("선형 탐색 : " + target + "회 탐색 시행 \t 이진 탐색 : " + answer + "회 시행");
}
public static int binarySearch(int start,int end,int target,int cnt){
int mid = (start+end)/2;
//중앙값이 원하는 값이면 반환
if(mid == target){
return cnt;
}
//타겟이 중앙값 보다 왼쪽
if( mid > target){
//기준 범위가 왼쪽이 될 수 있게 end 변경
end = mid -1;
}else{
//타겟이 중앙값 보다 오른쪽
//기준 범위가 오른쪽이 될 수 있게 start 변경
start = mid+1;
}
int result = binarySearch(start,end,target,cnt+1);
return result;
}
}
결과
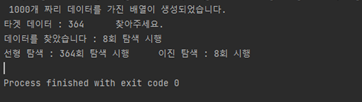
포스팅에 문제가 있거나, 설명이 잘못된 부분 지적 환영합니다.
읽어주셔서 감사합니다.
'공부 > JAVA' 카테고리의 다른 글
| [JAVA] 인터페이스(Interface) JAVA 개념을 부숴주마 (0) | 2021.08.30 |
|---|---|
| [JAVA] 기본개념 Stack 영역과 Heap 영역 (0) | 2021.08.25 |
| [JAVA]상속 (Inheritance) JAVA 개념을 부숴주마 (0) | 2021.08.23 |
| [JAVA] CMD에서 실행 시 오류나는 이유, UnsupportedClassVersionError (0) | 2021.08.22 |
| [JAVA] 자료형 - 기본형(Primitive type)과 참조형(Reference type) (0) | 2021.08.09 |
- Total
- Today
- Yesterday
- 그래프 탐색
- db
- 아기상어나쁜상어
- looker core
- DP
- 아기상어미워
- 자바
- 재귀
- value annotation
- Database
- 프로그래머스
- 카카오
- 실패일기
- 코딩테스트
- 프로그래머스 문제정복
- looker instance 접속
- 플루이드 와샬
- java
- 하루 회고
- Spring
- 브루트포스
- 백준
- JNDI연동
- DFS
- Python
- dml
- 9019
- BFS
- 파이썬
- 유클리드-호제법
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
