티스토리 뷰
자료구조 스터디 - Tree 구조 문제 풀이
BaekJoon level : Gold2

링크
https://www.acmicpc.net/problem/2250
2250번: 트리의 높이와 너비
첫째 줄에 노드의 개수를 나타내는 정수 N(1 ≤ N ≤ 10,000)이 주어진다. 다음 N개의 줄에는 각 줄마다 노드 번호와 해당 노드의 왼쪽 자식 노드와 오른쪽 자식 노드의 번호가 순서대로 주어진다.
www.acmicpc.net
문제
이진트리를 다음의 규칙에 따라 행과 열에 번호가 붙어있는 격자 모양의 틀 속에 그리려고 한다. 이때 다음의 규칙에 따라 그리려고 한다.
이진트리에서 같은 레벨(level)에 있는 노드는 같은 행에 위치한다.
한 열에는 한 노드만 존재한다.
임의의 노드의 왼쪽 부트리(left subtree)에 있는 노드들은 해당 노드보다 왼쪽의 열에 위치하고, 오른쪽 부트리(right subtree)에 있는 노드들은 해당 노드보다 오른쪽의 열에 위치한다.
노드가 배치된 가장 왼쪽 열과 오른쪽 열 사이엔 아무 노드도 없이 비어있는 열은 없다.
이와 같은 규칙에 따라 이진트리를 그릴 때 각 레벨의 너비는 그 레벨에 할당된 노드 중 가장 오른쪽에 위치한 노드의 열 번호에서 가장 왼쪽에 위치한 노드의 열 번호를 뺀 값 더하기 1로 정의한다. 트리의 레벨은 가장 위쪽에 있는 루트 노드가 1이고 아래로 1씩 증가한다.
아래 그림은 어떤 이진트리를 위의 규칙에 따라 그려 본 것이다. 첫 번째 레벨의 너비는 1, 두 번째 레벨의 너비는 13, 3번째, 4번째 레벨의 너비는 각각 18이고, 5번째 레벨의 너비는 13이며, 그리고 6번째 레벨의 너비는 12이다.
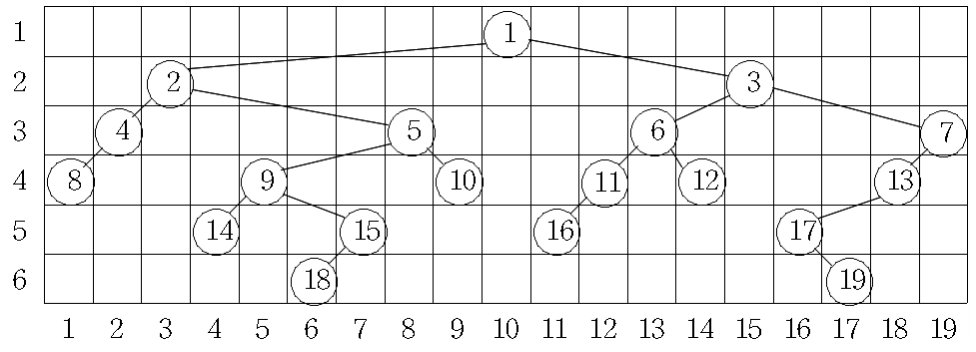
우리는 주어진 이진트리를 위의 규칙에 따라 그릴 때에 너비가 가장 넓은 레벨과 그 레벨의 너비를 계산하려고 한다. 위의 그림의 예에서 너비가 가장 넓은 레벨은 3번째와 4번째로 그 너비는 18이다. 너비가 가장 넓은 레벨이 두 개 이상 있을 때는 번호가 작은 레벨을 답으로 한다. 그러므로 이 예에 대한 답은 레벨은 3이고, 너비는 18이다.
임의의 이진트리가 입력으로 주어질 때 너비가 가장 넓은 레벨과 그 레벨의 너비를 출력하는 프로그램을 작성하시오
입력
첫째 줄에 노드의 개수를 나타내는 정수 N(1 ≤ N ≤ 10,000)이 주어진다. 다음 N개의 줄에는 각 줄마다 노드 번호와 해당 노드의 왼쪽 자식 노드와 오른쪽 자식 노드의 번호가 순서대로 주어진다. 노드들의 번호는 1부터 N까지이며, 자식이 없는 경우에는 자식 노드의 번호에 -1이 주어진다.
출력
첫째 줄에 너비가 가장 넓은 레벨과 그 레벨의 너비를 순서대로 출력한다. 너비가 가장 넓은 레벨이 두 개 이상 있을 때에는 번호가 작은 레벨을 출력한다.
접근방법
각 레벨이 가진 노드 들 중 너비 차이가 가장 클 때, 너비와 레벨을 구하는 문제이다. 해당 문제를 풀기 위해서는 그래프 문제임을 인지하고, 풀이하기 위해 어떤 정보가 필요한지, 노드를 어떻게 구성해야 할지 고민해야 한다. 또한 그러한 노드를 어떻게 탐색하여 길이를 구할지 생각해보아야 한다. 고민을 충분히 한 뒤, 풀이로 들어가자.
풀이
타 블로거님들의 해설 자료들을 보면서, 비교해보았는데, 대부분 순회 방식을 이용하여, 방문순서대로 노드에 value를 삽입하여 문제를 해결했다. 본인은 이와 해결방법이 다르니, 순회의 방식으로 구현하시려는 분들은 다른 해설을 이용하는 것이 좋을 것 같다.
해당 문제를 풀기 위해 필요한 정보부터 생각했다. 입력으로 들어오는 것은 노드의 갯수와 각 노드들이 가진 자식들의 관계만 주어진다. 문제에서 요구하는 레벨과 너비를 구하기 위해서는 각 노드가 길이와 레벨에 대한 정보를 가지고 있어야 한다고 생각했다. 따라서 각 노드가 가져가야 할 정보를 정의하고 그다음 해결 순서를 정리했다.
각 노드가 가지고있어야 할 정보
- 부모 노드 번호
- 자기 자신 번호
- 왼쪽 자식 번호
- 오른쪽 자식 번호
- 레벨
- 거리
해결 순서
- 각 노드가 가진 거리를 정리한다.
- 레벨별로 노드가 가진 거리를 정리한다.
- 가장 큰 거리차를 보이는 레벨과 값을 출력한다.
여기서 거리를 정의하는 것이 까다로웠다. 문제의 예시를 이용한다면, N개의 노드가 있다면, N길이에 노드가 하나씩 배치되어야 하는 구조이지만, 최상단 루트 노드의 길이가 고정되지 않으니, 길이를 정의하기가 까다로웠다. 그래서 본인은 상대 경로를 이용했다.
문제가 요구하는 것은 가장 큰 너비이다.
이 말은 해당 노드의 거리값이 중요한 것이 아니라, 노드 간의 거리 차가 우리가 구하는 값이며, 의미를 갖는다고 해석할 수 있다. 문제의 예를 들자면, 레벨 3의 노드 4번이 굳이 2 가아니라 -8 이어도 상관없다, 노드 7번이 9라면. 즉, 거리의 차이만 보증할 수 있다면, 각 노드 거리가 갖는 값은 뭐가 되어도 상관없다. 이러한 이유로 본인은 루트노드를 0으로 기준을 잡고, 거리를 구했다.
루트 노드의 거리를 0으로 잡았다 하더라도, 모든 노드에 대해 한번에 길이를 설정할 수 없다. 자식 노드가 왼쪽에 들어가는지, 오른쪽에 들어가는지에 따라 거리가 달라지기 때문에, 본인은 상대 경로와 DFS를 이용하여 이 부분을 해결했다. DFS의 특징은 리프 노드까지 우선적으로 탐색하는 것이 특징이므로, 리프 노드부터 경로를 파악한다면, 더 이상 자식 노드에 대해서 생각하지 않아도 된다.
그러나 이 방식은 단점 또한 존재한다. DFS이기 때문에 절대경로를 이용하기 어렵기 때문이다. DFS 특성상 리프 노드 값부터 거리를 구하게 되기 때문에 아직 계산도 되지 않은 부모 노드와 리프 노드의 거리 값을 사용할 수 없다. 따라서 각 노드가 부모 노드와의 상대적인 거리 차이만 가지고 있도록 일단 세팅해둔다.

위 그림을 예로 노드5번은 부모 노드 2번보다는 +5의 값을 지닌다. 이처럼 자기 부모 노드와의 상대 거리만 갖고 있다면, 추후 루트 노드부터 순차적으로 계산하면서 절대 경로로 변환이 가능하다.
위 과정을 통해 모든 노드가 상대경로값을 가지게 된다. 이제 모든 상대 경로 값을 절대 경로 값으로 바꾸어주면 거리에 대한 문제는 해결된다. 절대 경로로 바꾸는 방법은 간단하다. 루트 노드의 거리를 0으로 정의했기 때문에, 부모에 값을 가져와 재귀적으로 모든 노드들의 상대 경로 값을 절대 경로로 바꾸어주기만 하면 된다.
정리된 노드들을 레벨별로 Hashmap에 두고 최대 최소의 차를 구한뒤 답을 도출하면 문제는 해결된다.
코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
public class Main {
MyNode[] myNodes;
public static void main(String[] args) throws IOException {
Main test = new Main();
}
public Main() throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer stk;
int cnt_Node = Integer.parseInt(br.readLine());
//노드 갯수+1 만큼 생성(인덱스값 맞출 목적)
myNodes = new MyNode[cnt_Node + 1];
//key : level , value : distances 레벨당 가진 길이를 저장하는 맵
HashMap<Integer, ArrayList<Integer>> dist_per_lv = new HashMap<>();
//부모 노드 좌표 -1로 초기화
for (int i = 1 ; i <=cnt_Node ;i++){
myNodes[i] = new MyNode(i,-1);
}
//입력 및 노드 관계생성
for (int i = 0; i < cnt_Node; i++) {
stk = new StringTokenizer(br.readLine(), " ");
int self = Integer.parseInt(stk.nextToken());
int left = Integer.parseInt(stk.nextToken());
int right = Integer.parseInt(stk.nextToken());
myNodes[self].left = left;
myNodes[self].right = right;
if(left != -1){
myNodes[left].parents = self;
}
if(right != -1){
myNodes[right].parents = self;
}
}
int root = 1;
//루트노드만 부모노드가 -1임을 이용하여 찾음
for (int i = 1 ; i <=cnt_Node ;i++){
if(myNodes[i].parents ==-1){
root = i;
}
}
//루트노드를 기준으로 DFS
getNodeCnt( root, 1, 0, 0);
//상대경로를 절대경로로 변환
setAbsDistance(root);
//맵에 레벨별로 distance 정리
for (int i = 1 ; i < myNodes.length ; i++){
if(!dist_per_lv.containsKey(myNodes[i].depths)){
dist_per_lv.put(myNodes[i].depths,new ArrayList<>());
}
dist_per_lv.get(myNodes[i].depths).add(myNodes[i].abs_dist);
}
int depths =0 , max =0;
//레벨별로 최대 최소값 차를 구하여 큰값을 저장
for (Map.Entry<Integer, ArrayList<Integer>> entry : dist_per_lv.entrySet()){
int data =Collections.max(entry.getValue())-Collections.min(entry.getValue())+1;
if(max < data){
depths = entry.getKey();
max = data;
}
}
System.out.println(depths+" "+max);
}
//dfs로 순회하면서, level과 부모노드와의 상대거리를 저장함
private int getNodeCnt( int cur, int levels, int parent, int ways) {
//없는 노드라면 리턴
if (cur == -1) {
return 0;
}
//자신 기준 왼쪽과 오른쪽거리를 구분
int left = 0;
int right = 0;
//dfs ways: 1 -> 왼쪽 2-> 오른쪽
left = getNodeCnt( myNodes[cur].left, levels + 1, cur, 1);
right = getNodeCnt( myNodes[cur].right, levels + 1, cur, 2);
int rel_dist = 0;
//본인 노드를 기준으로 부모노드와의 차이 계산
if (ways == 1) {
//본인노드 기준 부모노드가 오른쪽에 있으므로
//부모에 비해 음수 값을 가짐
rel_dist = -(1 + right);
} else if (ways == 2) {
//본인노드 기준 부모노드가 왼쪽에 있으므로
//부모에 비해 양수 값을 가짐
rel_dist = 1 + left;
}
//상대 거리 및 level을 를 해당 노드에 저장
myNodes[cur].abs_dist = rel_dist;
myNodes[cur].depths = levels;
return left + right + 1;
}
//상대경로를 절대경로로 바꿔주는 재귀 메소드
private void setAbsDistance(int cur){
if (cur ==-1){
return;
}
//현재 가지고 있는 상대 경로 값
int ac = myNodes[cur].abs_dist;
//부모가 있다면 부모가 가진 값과 합산
if(myNodes[cur].parents !=-1){
ac += myNodes[myNodes[cur].parents].abs_dist;
}
myNodes[cur].abs_dist = ac;
//재귀적으로 수행
setAbsDistance(myNodes[cur].left);
setAbsDistance(myNodes[cur].right);
}
class MyNode {
int parents;
int myNo;
int left = -1;
int right = -1;
int abs_dist;
int depths;
public MyNode(int myNo, int parents) {
this.myNo = myNo;
this.parents = parents;
}
}
}결과

해당 문제를 풀면서 재귀 함수를 통해 Bottom-up 방식으로 상대거리를 구하고, Top-Down 방식으로 절대거리를 구하는 두 가지 방식을 모두 써본 좋은 문제였다. 거리를 구하기 위해 DFS를 두 번이나 사용했기에, 시간 초과 이슈에 대한 걱정을 많이 했는데, 오히려 너무나도 준수한 결과를 보여줘서 고생한 보람을 느낀 문제였다. :D
포스팅에 문제가 있거나, 설명이 잘못된 부분 지적 환영합니다.
더 나은 퀄리티의 콘텐츠를 제공할 수 있도록 노력하겠습니다.
읽어주셔서 감사합니다.
'공부 > 코딩 테스트 준비' 카테고리의 다른 글
| [프로그래머스] 추석트래픽 - JAVA (0) | 2021.12.17 |
|---|---|
| [프로그래머스] 모의고사 - Python (0) | 2021.12.14 |
| [백준] 14500 - 테트로미노 JAVA (0) | 2021.10.17 |
| [백준] 11053 - 가장 긴 증가하는 부분 수열 JAVA (0) | 2021.10.16 |
| [백준] 6064 - 카잉 달력 JAVA (0) | 2021.10.15 |
- Total
- Today
- Yesterday
- db
- 9019
- 유클리드-호제법
- Spring
- 프로그래머스
- 백준
- 코딩테스트
- looker core
- 하루 회고
- 플루이드 와샬
- 아기상어미워
- DP
- 그래프 탐색
- 카카오
- Python
- 재귀
- value annotation
- Database
- java
- looker instance 접속
- DFS
- 실패일기
- 파이썬
- dml
- 자바
- 아기상어나쁜상어
- 프로그래머스 문제정복
- BFS
- 브루트포스
- JNDI연동
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
